1228. Сложить все

Стоимость сложения двух чисел равна их сумме. То есть, чтобы прибавить 10 к 1, следует заплатить 11. В задаче требуется сложить все заданные числа так, чтобы потратить наименьшую сумму денег.

Например, складывать числа 1, 2 и 3 можно одним из трех способов:

· 1 + 2 = 3 (стоимость = 3), 3 + 3 = 6 (стоимость = 6). Всего = 9

· 1 + 3 = 4 (стоимость = 4), 2 + 4 = 6 (стоимость = 6). Всего = 10

· 2 + 3 = 5 (стоимость = 5), 1 + 5 = 6 (стоимость = 6). Всего = 11

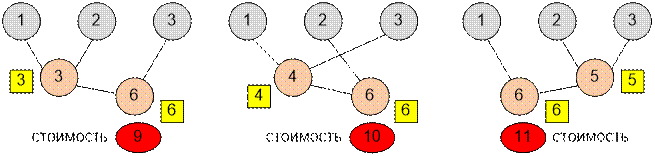
Первый способ сложения является самым дешевым.

Вход. Первая строка содержит натуральное число n (2 ≤ n ≤ 10⁵). Вторая строка содержит n целых неотрицательных чисел, каждое из которых не превышает 10⁵.

Выход. Выведите наименьшую стоимость сложения всех чисел.

Пример входа	Пример выхода
4 1 2 3 4	19

РЕШЕНИЕ

жадность

Анализ алгоритма

Каждый раз следует складывать два наименьших числа. Таким образом, суммарная стоимость сложения всех n чисел будет минимальной. Поскольку числа могут повторяться, их удобно хранить в мультимножестве.

Пример

Для минимизации стоимости сложения будем складывать числа в следующем порядке:

1. Складываем 1 и 2, получим 3. Стоимость сложения 3.

2. Складываем 3 и 3, получим 6. Стоимость сложения 6.

3. Складываем 4 и 6, получим 10. Стоимость сложения 10.

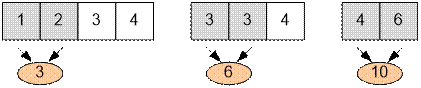
Общая стоимость сложения равна 3 + 6 + 10 = 19.

Реализация алгоритма

Входные числа храним в мультимножестве s (числа могут повторяться). Два наименьших числа всегда располагаются в начале мультимножества.

multiset<long long> s;

Читаем количество чисел n.

scanf("%lld",&n);

Читаем последовательность слагаемых и добавляем их в мультимножество s.

for (i = 0; i < n; i++)

{

scanf("%lld",&x);

s.insert(x);

}

В переменной res вычисляем стоимость сложений всех чисел.

res = 0;

Пока в мультимножестве s больше одного числа, извлекаем и складываем два его наименьших элемента и добавляем их сумму обратно в s. Стоимость сложения чисел a и b равна a + b, и она прибавляется к res.

while (s.size() > 1)

{

a = *s.begin(); s.erase(s.begin());

b = *s.begin(); s.erase(s.begin());

s.insert(a + b);

res += a + b;

}

Когда в мультимножестве остаётся только одно число, выводим ответ – значение переменной res.

printf("%lld\n",res);

Реализация при помощи очереди с приоритетами

Объявим очередь с приоритетами pq, в начале которой всегда находится наименьший элемент.

priority_queue<long long, vector<long long>, greater<long long> > pq;

Читаем количество чисел n.

scanf("%lld",&n);

Читаем последовательность слагаемых и добавляем их в очередь с приоритетами pq.

scanf("%lld",&n);

for (i = 0; i < n; i++)

{

scanf("%lld",&x);

pq.push(x);

}

В переменной res вычисляем стоимость сложений всех чисел.

res = 0;

Пока в очереди pq больше одного числа, извлекаем и складываем два его наименьших элемента и добавляем их сумму обратно в pq. Стоимость сложения чисел a и b равна a + b, и она прибавляется к res.

while (pq.size() > 1)

{

a = pq.top(); pq.pop();

b = pq.top(); pq.pop();

pq.push(a + b);

res += a + b;

}

Когда в очереди остаётся только одно число, выводим ответ – значение переменной res.

printf("%lld\n",res);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

PriorityQueue<Long> pq = new PriorityQueue<Long>();

for(int i = 0; i < n; i++)

{

long val = con.nextLong();

pq.add(new Long(val));

}

long Result = 0;

while(pq.size() > 1)

{

long a = pq.poll();

long b = pq.poll();

pq.add(a + b);

Result += a + b;

}

System.out.println(Result);

}

}

Python реализация

Объявим очередь с приоритетами q, в начале которой всегда находится наименьший элемент.

from queue import PriorityQueue

q = PriorityQueue()

Читаем входные данные.

n = int(input())

lst = map(int,input().split())

Добавим слагаемые в очередь q.

for x in lst:

q.put(x)

В переменной res вычисляем стоимость сложений всех чисел.

res = 0

Пока в очереди q больше одного числа, извлекаем и складываем два его наименьших элемента и добавляем их сумму обратно в q. Стоимость сложения чисел a и b равна a + b, и она прибавляется к res.

while q.qsize() > 1:

a = q.get()

b = q.get()

q.put(a + b)

res += a + b

Когда в очереди остаётся только одно число, выводим ответ – значение переменной res.

print(res)